Answer: 0.1587
Explanation:
Given : The foreman of a bottling plant has observed that the amount of soda in each 16-ounce bottle is actually a normally distributed random variable, with
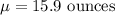
Standard deviation :
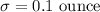
Let x be the amount of soda in a randomly selected bottle.
Z-score :
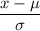

The probability that the bottle will contain more than 16 ounces using standardized normal distribution table :
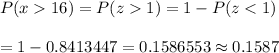
Hence, the probability that the bottle will contain more than 16 = 0.1587