Question

A uniform disk turns at 5.00 rev/s around a frictionless spindle. A non-rotating rod, of the same mass as the disk and length equal to the disk’s diameter, is dropped onto the freely spinning disk. They then turn together around the spindle with their centers superposed. What is the angular frequency in of the rev/scombination?

Answer 1

Final angular speed equals 3 revolutions per second

Step-by-step explanation:

We shall use conservation of angular momentum principle to solve this problem since the angular momentum of the system is conserved

`L_(disk)=I_(disk)\omega \\\\L_(disk)=(1)/(2)mr^(2)\\\therefore L_(disk)=(1)/(2)mr^(2)*10rad/sec`

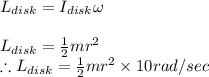
After the disc and the dropped rod form a single assembly we have the final angular momentum of the system as follows

`L_(final)=I_(disk+rod)* \omega_(f) \\\\I_(disk+rod)=(1)/(2)mr_(disc)^(2)+(1)/(12)mL_(rod)^(2)\\I_(disk+rod)=(1)/(2)mr_(disc)^(2)+(1)/(12)m* (2r_(disc))^(2)\\\\I_(disk+rod)=(1)/(2)mr_(disc)^(2)+(1)/(3)mr_(disc)^(2)\\\\L_(final)=(5mr_(disc)^(2))/(6)* \omega _(f)\\\\`

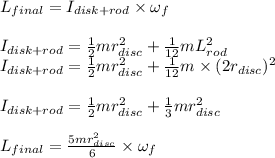
Equating initial and final angular momentum we have

`(5mr_(disc)^(2))/(6)* \omega _(f)=(1)/(2)m_(disc)* r_(disc)^(2)* 10\pi rad/sec`

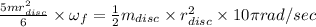
Solving for
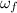`\omega_(f)` we get

`\omega_(f)=6\pi rad/sec`

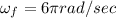
Thus no of revolutions in 1 second are 6π/2π

No of revolutions are 3 revolutions per second