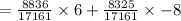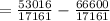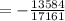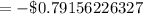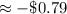Question

Suppose a basketball player has made 282 out of 393 free throws. If the player makes the next 2 free throws, I will pay you $6. Otherwise you pay me $8.Step 1 of 2 :Find the expected value of the proposition. Round your answer to two decimal places. Losses must be expressed as negative values.

Answer 1

-$ 0.79

Explanation:

Since, the player has made 282 out of 393 free throws,

So, the probability of a free throw =
`(282)/(393)`,

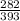Thus, the probability of 2 free throws =
`(282)/(393)* (282)/(393)=(8836)/(17161)`

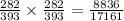
And, the probability of not getting 2 free throws =
`1-(8836)/(17161)=(8325)/(17161)`

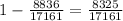
Given, the price of winning ( getting 2 free throws ) is $6 while the price of losing ( not getting 2 free throws ) is - $ 8 ( ∵ there is a loss of $ 8 ),

Hence, the expected value of the proposition = probability of winning × winning value + probability of losing × losing value

`= (8836)/(17161)* 6 + (8325)/(17161)* -8`

`=(53016)/(17161)-(66600)/(17161)`

`=-(13584)/(17161)`

`=-\$ 0.79156226327`

`\approx -\$ 0.79`