Question

(1 pt) In a study of red/green color blindness, 950 men and 2050 women are randomly selected and tested. Among the men, 89 have red/green color blindness. Among the women, 6 have red/green color blindness. Construct the 99% confidence interval for the difference between the color blindness rates of men and women.

Answer 1

Answer: (0.066,0.116)

Explanation:

The confidence interval for proportion is given by :-

`p_1-p_2\pm z_(\alpha/2)\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2)}`

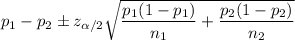
Given : The proportion of men have red/green color blindness =
`p_1=(89)/(950)\approx0.094`

The proportion of women have red/green color blindness =
`p_2=(6)/(2050)\approx0.003`

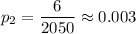
Significance level :
`\alpha=1-0.99=0.01`

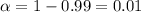
Critical value :
`z_(\alpha/2)=z_(0.005)=\pm2.576`

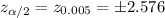
Now, the 99% confidence interval for the difference between the color blindness rates of men and women will be:-

`(0.094-0.003)\pm (2.576)\sqrt{(0.094(1-0.094))/(950)+(0.003(1-0.003))/(2050)}\approx0.091\pm 0.025\\\\=(0.09-0.025,0.09+0.025)=(0.066,\ 0.116)`

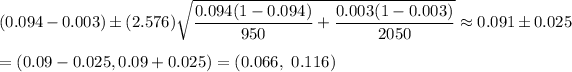
Hence, the 99% confidence interval for the difference between the color blindness rates of men and women= (0.066,0.116)