Answer:
840.02 square inches ( approx )
Explanation:
Suppose x represents the side of each square, cut from the corners of the sheet,
Since, the dimension of the sheet are,
31 in × 17 in,
Thus, the dimension of the rectangular box must are,
(31-2x) in × (17-2x) in × x in
Hence, the volume of the box would be,
V = (31-2x) × (17-2x) × x
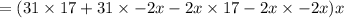
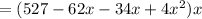
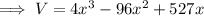
Differentiating with respect to x,
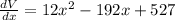
Again differentiating with respect to x,
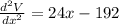
For maxima or minima,
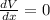
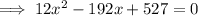
By the quadratic formula,
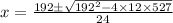
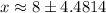
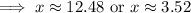
Since, at x = 12.48,
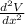 = Positive,
= Positive,
While at x = 3.52,
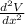 = Negative,
= Negative,
Hence, for x = 3.52 the volume of the rectangle is maximum,
Therefore, the maximum volume would be,
V(3.5) = (31-7.04) × (17-7.04) × 3.52 = 840.018432 ≈ 840.02 square inches