Question

The mean per capita income is 15,451 dollars per annum with a variance of 298,116. What is the probability that the sample mean would differ from the true mean by less than 22 dollars if a sample of 350 persons is randomly selected? Round your answer to four decimal places.

Answer 1

Answer: 0.5467

Explanation:

Let X be the random variable that represents the income (in dollars) of a randomly selected person.

Given :
`\mu=15451`

`\sigma^2=298116\\\\\Rightarrow\ \sigma=√(298116)=546`

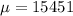
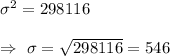
Sample size : n=350

z-score :
`(x-\mu)/((\sigma)/(√(n)))`

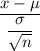
To find the probability that the sample mean would differ from the true mean by less than 22 dollars, the interval will be

`\mu-22,\ \mu+22\\\\=15,451 -22,\ 15,451 +22\\\\=15429,\ 15473`

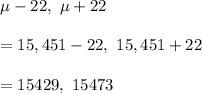
For x=15429

`z=(15429-15451)/((546)/(√(350)))\approx-0.75`

For x=15473

`z=(15473-15451)/((546)/(√(350)))\approx0.75`

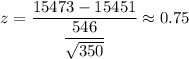
The required probability :-

`P(15429<X<15473)=P(-0.75<z<0.75)\\\\=1-2(P(z<0.75))=1-2(0.2266274)=0.5467452\approx0.5467`

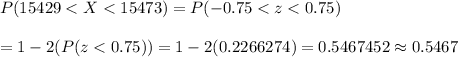
Hence, the required probability is 0.5467.