Question

Use a half-angle identity to find the exact value of tan 165 degrees

Answer 1

√3 - 2.

Explanation:

Let A = 330 degrees so A/2 = 165 degrees.

tan A/2 = (1 - cos A) / sin A

tan 165 = (1 - cos 330) / sin 330

= (1 - √3/2) / (-1/2)

= -2(1 - √3/2)

= -2 + 2 * √3/2

= √3 - 2.

Answer 2

`√(3)` - 2

Explanation:

Using the half- angle identity

tan(
`(x)/(2)` ) =
`(sinx)/(1+cosx)`

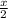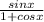
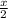`(x)/(2)` = 165° ⇒ x = 330°

sin330° = - sin30° = -
`(1)/(2)`

cos330° = cos30° =
`(√(3) )/(2)`

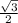
tan165° =
`(sin330)/(1+cos330)`

=
`(-(1)/(2) )/(1+(√(3) )/(2) )`

= -
`(1)/(2)` ×
`(2)/(2+√(3) )`

= -
`(1)/(2+√(3) )`

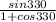
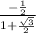
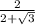
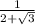
Rationalise by multiplying numerator/ denominator by the conjugate of the denominator

The conjugate of 2 +
`√(3)` is 2 -
`√(3)`, hence

tan 165°

= -
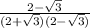
`(2-√(3) )/((2+√(3))(2-√(3))  )`

= -
`(2-√(3) )/(4-3)`

= - (2 -
`√(3)` )

= - 2 +
`√(3)` =
`√(3)` - 2