Question

A 3.9 kg block is pushed along a horizontal floor by a force ModifyingAbove Upper F With right-arrow of magnitude 27 N at a downward angle θ = 40°. The coefficient of kinetic friction between the block and the floor is 0.22. Calculate the magnitudes of (a) the frictional force on the block from the floor and (b) the block’s acceleration.

Answer 1

a) 12.23 N

b) 2.2 m/s²

Step-by-step explanation:

m = mass of the block = 3.9 kg

F = applied force = 27 N

θ = angle of the applied force with the horizontal = 40°

μ = Coefficient of kinetic friction = 0.22

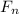`F_(n)` = normal force

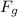`F_(g)` = weight of the block = mg

Along the vertical direction, force equation is given as

`F_(n)` = F Sinθ +
`F_(g)`

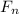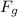
`F_(n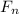)` = F Sinθ + mg

Kinetic frictional force is given as

f = μ
`F_(n)`

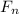
f = μ (F Sinθ + mg)

f = (0.22) (27 Sin40 + (3.9)(9.8))

f = 12.23 N

b)

Force equation along the horizontal direction is given as

F Cosθ - f = ma

27 Cos40 - 12.23 = 3.9 a

a = 2.2 m/s²