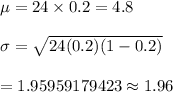Question

b. Suppose 20​% of all balls produced by a particular manufacturer are less than 1.680 inches in​ diameter, and assume that the number of such​ balls, x, in a sample of two dozen balls can be adequately characterized by a binomial probability distribution. Find the mean and standard deviation of the binomial distribution.

Answer 1

Answer: Mean = 4.8

Standard deviation = 1.96

Explanation:

The mean and standard deviation of the binomial distribution is given by :-

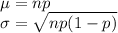`\mu=np\\\sigma=√(np(1-p))`, where n is the total number of trials , p is the the probability of success.

Given : The probability that the produced by a particular manufacturer are less than 1.680 inches in​ diameter = 20%=0.2

Sample size : n=24 [since 1 dozen = 12]

Now, the mean and standard deviation of the binomial distribution is given by :-

`\mu=24*0.2=4.8\\\\\sigma=√(24(0.2)(1-0.2))\\\\=1.95959179423\approx1.96`