Answer:
Blank 1: 3 is the remainder
Blank 2: not a factor
Explanation:
If p(x)=(x-7)(x^2-2x+4)+3, then dividing both sides by (x-7) gives:
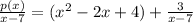 .
.
The quotient is
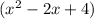 .
.
The remainder is
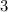 .
.
The divisor is
 .
.
The dividend is
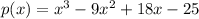 .
.
It is just like with regular numbers.
 as a whole number is
as a whole number is
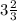 .
.
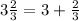 where 3 is the quotient and 2 is the remainder when 11 is divided by 3.
where 3 is the quotient and 2 is the remainder when 11 is divided by 3.
Here is the division just for reminding purposes:
3 <--quotient
----
divisor-> 3 | 11 <--dividend
-9
---
2 <---remainder
Anyways just for fun, I would like to verify the given equation of
p(x)=(x-7)(x^2-2x+4)+3.
I would like to do by dividing myself.
I could use long division, but I have a choice to use synthetic division since we are dividing by a linear factor.
Since we are dividing by x-7, 7 goes on the outside:
x^3-9x^2+18x -25
7 | 1 -9 18 -25
| 7 -14 28
-------------------------------
1 -2 4 3
We have confirmed what they wrote is totally correct.
The quotient is
 while the remainder is 3.
while the remainder is 3.
If p/(x-7) gave a remainder of 0 then we would have said (x-7) was a factor of p.
It didn't so it isn't.
Just like with regular numbers. Is 3 a factor of 6? Yes, because the remainder of dividing 6 by 3 is 0.