Explanation:
sin^2x = 2cotx sin^2x
Rewrite right side as fractions:
sin^2x =
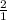 *
*
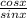 *
*
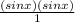
Multiply together
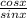 and
and
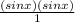 :
:
sin^2x =
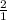 *
*
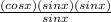
Cancel out sinx on top and bottom:
sin^2x =
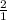 *
*
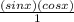
Multiply together 2 and (sinx)(cosx):
sin^2x = 2sinxcosx
Substitute sin^2x in for 2sinxcosx:
sin^2x = sin^2x