Question

If h(x) = (fog) (x) and h(x) = 4 square root x+7, find g(x) if f(x) = 4 square root x+ 1

Answer 1

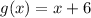`g(x)=x+6` is the answer

given

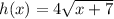`h(x)=4√(x+7)` and
`f(x)=4√(x+1)`.

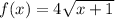Explanation:

`h(x)=(f \circ g)(x)`

`h(x)=f(g(x))`

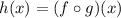
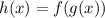
Inputting the given function for h(x) into the above:

`4√(x+7)=f(g(x))`

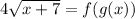
Now we are plugging in g(x) for x in the expression for f which is
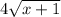`4√(x+1)` which gives us
`4√(g(x)+1)`:

`4√(x+7)=4√(g(x)+1)`

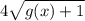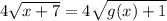
We want to solve this for g(x).

If you don't like the looks of g(x) (if you think it is too daunting to look at), replace it with u and solve for u.

`4√(x+7)=4√(u+1)`

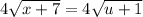
Divide both sides by 4:

`√(x+7)=√(u+1)`

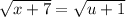
Square both sides:

`x+7=u+1`

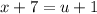
Subtract 1 on both sides:

`x+7-1=u`

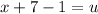
Simplify left hand side:

`x+6=u`

`u=x+6`

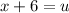
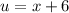
Remember u was g(x) so you just found g(x) so congratulations.

`g(x)=x+6`.

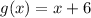Let's check it:

`(f \circ g)(x)`

`f(g(x))`

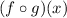
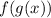
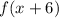`f(x+6)` I replace g(x) with x+6 since g(x)=x+6.

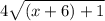`4√((x+6)+1)` I replace x in f with (x+6).

`4√(x+6+1)`

`4√(x+7)`

`h(x)`

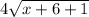
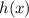
The check is done. We have that
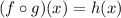`(f \circ g)(x)=h(x)`.