Question

Use the Polynomial Identity below to help you create a list of 10 Pythagorean Triples:

(x²+y²)² = (x²-y²)² + (2xy)²
Hint #1: c² = a² + b²
Hint #2: pick 2 positive integers x and y, where x > y

Answer 1

(3,4,5)

(6,8,10)

(5,12,13)

(8,15,17)

(12,16,20)

(7,24,25)

(10,24,26)

(20,21,29)

(16,30,34)

(9,40,41)

Just choose 2 numbers from {1,2,3,4,5,6,7,8,...} and make sure the one you input for x is larger.

Post the three in the comments and I will check them for you.

Explanation:

We need to choose 2 positive integers for x and y where x>y.

Positive integers are {1,2,3,4,5,6,7,.....}.

I'm going to start with (x,y)=(2,1).

x=2 and y=1.

`(2^2+1^2)^2=(2^2-1^2)^2+(2\cdot2\cdot1)^2`

`(4+1)^2=(4-1)^2+(4)^2`

`(5)^2=(3)^2+(4)^2`

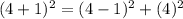
So one Pythagorean Triple is (3,4,5).

I'm going to choose (x,y)=(3,1).

x=3 and y=1.

`(3^2+1^2)^2=(3^2-1^2)^2+(2\cdot3\cdot1)^2`

`(9+1)^2=(9-1)^2+(6)^2`

`(10)^2=(8)^2+(6)^2`

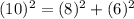
So another Pythagorean Triple is (6,8,10).

I'm going to choose (x,y)=(3,2).

x=3 and y=2.

`(3^2+2^2)^2=(3^2-2^2)^2+(2\cdot3\cdot2)^2`

`(9+4)^2=(9-4)^2+(12)^2`

`(13)^2=(5)^2+(12)^2`

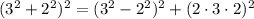
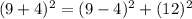
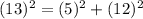
So another is (5,12,13).

I'm going to choose (x,y)=(4,1).

`(4^2+1^2)^2=(4^2-1^2)^2+(2\cdot4\cdot1)^2`

`(16+1)^2=(16-1)^2+(8)^2`

`(17)^2=(15)^2+(8)^2`

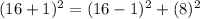
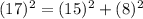
Another is (8,15,17).

I'm going to choose (x,y)=(4,2).

`(4^2+2^2)^2=(4^2-2^2)^2+(2\cdot4\cdot2)^2`

`(16+4)^2=(16-4)^2+(16)^2`

`(20)^2=(12)^2+(16)^2`

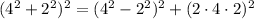
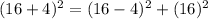
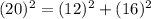
We have another which is (12,16,20).

I'm going to choose (x,y)=(4,3).

`(4^2+3^2)^2=(4^2-3^2)^2+(2\cdot4\cdot3)^2`

`(16+9)^2=(16-9)^2+(24)^2`

`(25)^2=(7)^2+(24)^2`

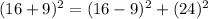
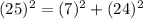
We have another is (7,24,25).

You are just choosing numbers from the positive integer set {1,2,3,4,... } and making sure the number you plug in for x is higher than the number for y.

I will do one more.

Let's choose (x,y)=(5,1).

`(5^2+1^2)^2=(5^2-1^2)^2+(2\cdot5\cdot1)^2`

`(25+1)^2=(25-1)^2+(10)^2`

`(26)^2=(24)^2+(10)^2`

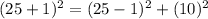
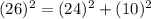
So (10,24,26) is another.

Let (x,y)=(5,2).

`(5^2+2^2)^2=(5^2-2^2)^2+(2\cdot5\cdot2)^2`

`(25+4)^2=(25-4)^2+(20)^2`

`(29)^2=(21)^2+(20)^2`

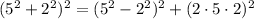
So another Pythagorean Triple is (20,21,29).

Choose (x,y)=(5,3).

`(5^2+3^2)^2=(5^2-3^2)^2+(2\cdot5\cdot3)^2`

`(25+9)^2=(25-9)^2+(30)^2`

`(34)^2=(16)^2+(30)^2`

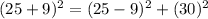
Another Pythagorean Triple is (16,30,34).

Let (x,y)=(5,4)

`(5^2+4^2)^2=(5^2-4^2)^2+(2\cdot5\cdot4)^2`

`(25+16)^2=(25-16)^2+(40)^2`

`(41)^2=(9)^2+(40)^2`

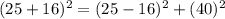
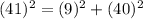
Another is (9,40,41).