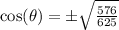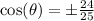Answer:
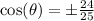
Explanation:
I don't know where
 is so there is going to be two possibilities for cosine value, one being positive while the other is negative.
is so there is going to be two possibilities for cosine value, one being positive while the other is negative.
A Pythagorean Identity is
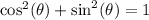 .
.
We are given
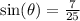 .
.
So we are going to input
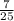 for the
for the
 :
:
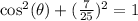
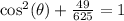
Subtract 49/625 on both sides:

Find a common denominator:
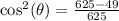

Square root both sides: