Question

Out of 100 people at a tennis match, 66% were rooting for the local champion. If two people were chosen at random from the crowd, what is the probability that at least one of them was not rooting for the champion?

Question 16 options:

22.7%

56.7%

59.2%

43.3%

Answer 1

56.7% is correct.

Explanation:

Answer 2

Approximately 56.7%.

Explanation:

Choose two people at random from the crowd and there will be two cases:

• Zero or one out of the two person was rooting for the champion, or
• both were rooting for the champion.

There's no third possible outcome. In other words, the two cases are mutually exclusive. Either the first or the second event is expected to happen. The sum of their probabilities shall equal to 1.

66 out of that 100 were rooting for the champion. The probability that both were rooting for the champion will be easier to find. The probability that the first person is rooting for the champion is equal to
`66/100`.

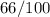After that first person was chosen from the crowd, the 65 out of the remaining 99 person in the crowd were chanting. The probability that the second person is rooting as well will equal to
`65/100`.

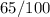Both event shall take place. The probability that both were rooting for the champion will equal to

`\displaystyle (66)/(100) * (65)/(99)`.

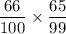The probability that one or zero out of the two persons were rooting will equal to

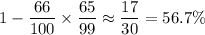`\displaystyle 1 - (66)/(100) * (65)/(99) \approx (17)/(30) = 56.7\%`.