Question

A wheel of moment of inertia of 5.00 kg∙m2 starts from rest and accelerates under a constant torque of 3.00 N∙m for 8.00 s. What is the wheel's rotational kinetic energy at the end of 8.00 s?

Answer 1

The wheel's rotational kinetic energy is 57.6 J.

Step-by-step explanation:

Given that,

Moment of inertia = 5.00 kg.m²

Torque = 3.00 N.m

Time = 8.00 s

We need to calculate the angular acceleration

Using formula of the torque act on the wheel

`\tau=I\alpha`

`\alpha=(\tau)/(I)`

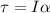
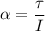
Where, I = moment of inertia

`\alpha` = angular acceleration

`\tau` = torque

Put the value into the formula

`\alpha=(3.00)/(5.00)`

`\alpha=0.6\ rad/s^2`

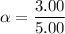
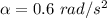
We need to calculate the final angular velocity

Initially wheel at rest so initial velocity is zero.

Using formula of angular velocity

`\alpha=(\omega_(f)-\omega_(i))/(t)`

`\omega_(f)=\omega_(i)+\alpha t`

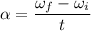
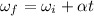
Put the value into the formula

`\omega_(f)=0+0.6*8.00`

`\omega_(f)=4.8\ rad/s`

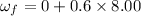
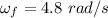
We need to calculate the rotational kinetic energy of the wheel

Using formula of the rotational kinetic energy

`K.E_(rot)=(1)/(2)I\omega^2`

`K.E_(rot)=(1)/(2)*5.00*(4.8)^2`

`K.E_(rot)=57.6\ J`

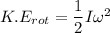
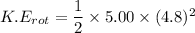
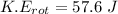
Hence, The wheel's rotational kinetic energy is 57.6 J.