Question

NEED HELP!!!
see picture*****

Answer 1

1. -10

2.
`x=1\pm√(2)i`

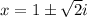
3. -1+2i

4. -3-7i

5. 13

6. rectangular coordinates are (-4.3,-2.5)

7. rectangular coordinates are (-2.5,4.3)

8. x^2 + y^2 = 8y

9. Polar coordinates of point (-3,0) are (3,180°)

10. Polar coordinates of point (1,1) are (√2,45°)

Explanation:

1) Simplify (2+3i)^2 + (2-3i)^2

Using formula (a+b)^2 = a^2+2ab+b^2

=((2)^2+2(2)(3i)+(3i)^2)+((2)^2-2(2)(3i)+(3i)^2)

=(4+12i+9i^2)+(4-12i+9i^2)

We know that i^2=-1

=(4+12i+9(-1))+(4-12i+9(-1))

=(4+12i-9)+(4-12i-9)

=(-5+12i)+(-5-12i)

=5+12i-5-12i

=-10

2. Solve x^2-2x+3 = 0

Using quadratic formula to find value of x

a=1, b=-2 and c=3

`x=(-b\pm√(b^2-4ac))/(2a)\\x=(-(-2)\pm√((-2)^2-4(1)(3)))/(2(1))\\x=(2\pm√(4-12))/(2)\\x=(2\pm√(-8))/(2)\\x=(2\pm2√(-2))/(2)\\x=(2\pm2√(2)i)/(2)\\x=2((1\pm√(2)i)/(2))\\x=1\pm√(2)i`

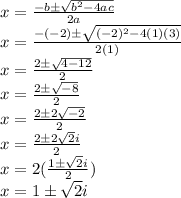
3. If u =1+3i and v =-2-i what is u+v

u+v = (1+3i)+(-2-i)

u+v = 1+3i-2-i

u+v = 1-2+3i-i

u+v = -1+2i

4. if u = 3-4i and v = 3i+6 what is u-v

u-v = (3-4i)-(3i+6)

u-v = 3-4i-3i-6

u-v = 3-6-4i-3i

u-v = -3-7i

5. if u=(3+2i) and v=(3-2i) what is uv?

uv = (3+2i)(3-2i)

uv = 3(3-2i)+2i(3-2i)

uv = 9-6i+6i-4i^2

uv = 9-4i^2

i^2=-1

uv = 9-4(-1)

uv = 9+4

uv = 13

6. Convert (5, 7π/6) to rectangular form

To convert polar coordinate into rectangular coordinate we use formula:

x = r cos Ф

y = r sin Ф

r = 5, Ф= 7π/6

x = r cos Ф

x = 5 cos (7π/6)

x = -4.3

y = r sin Ф

y = 5 sin (7π/6)

y = -2.5

So rectangular coordinates are (-4.3,-2.5)

7. Convert (5, 2π/3) to rectangular form

To convert polar coordinate into rectangular coordinate we use formula:

x = r cos Ф

y = r sin Ф

r = 5, Ф= 2π/3

x = r cos Ф

x = 5 cos (2π/3)

x = -2.5

y = r sin Ф

y = 5 sin (2π/3)

y = 4.33

So rectangular coordinates are (-2.5,4.33)

8. Convert r=8cosФ to rectangular form

r.r = (8 cos Ф)r

r^2 = 8 (cosФ)(r)

Let (cosФ)(r) = y and we know that r^2 = x^2+y^2

x^2 + y^2 = 8y

9. Convert(-3,0) to polar form

We need to find (r,Ф)

r = √x^2+y^2

r = √(-3)^2+(0)^2

r =√9

r = 3

and tan Ф = y/x

tan Ф = 0/-3

tan Ф = 0

Ф = tan^-1(0)

Ф = 0°

As Coordinates are in 2nd quadrant, so add 180° in the given angle

0+180 = 180°

So,Polar coordinates of point (-3,0) are (3,180°)

10) Convert (1,1) to polar form

We need to find (r,Ф)

r = √x^2+y^2

r = √(1)^2+(1)^2

r =√2

and tan Ф = y/x

tan Ф = 1/1

tan Ф = 1

Ф = tan^-1(1)

Ф = 45°

As Coordinates are in 1st quadrant, so Ф will be as found

So,Polar coordinates of point (1,1) are (√2,45°)