Question

Suppose that an experiment determines that the amount of work required for a Force field to move a particle from the point ( 1 , 2 ) to the point ( − 5 , 3 ) along the curve C 1 is 1.2 J and the work done by the field in moving the particle along another curve C 2 between the same two points is 1.4 J. What can you say about the field, and why? g

Answer 1

From the given information we can infer that the field is not conservative.

Step-by-step explanation:

For a conservative field the work done on an object in moving it from a position given by co-ordinates
`(x_(1),y_(1),z_(1))` to another position with co-ordinates
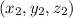`(x_(2),y_(2),z_(2))` shall be independent of the path we take in between to reach our final position (by definition of a conservative field). But in the given case since the initial and the final position of both the curves
`C_(1),C_(2)` coincide but the work done along both the paths is different thus we conclude that the field is not conservative.