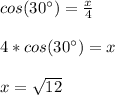Question

Please help me with this

Answer 1

Answer: second option.

Explanation:

By definition, the measure of any interior angle of an equilateral triangle is 60 degrees.

Based in this, we know that the measusre of the angle ∠SRT is:

`\angle SRT=(60\°)/(2)=30\°`

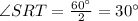
The, we can find the value of "y":

`y+12=30\\y=30-12\\y=18`

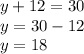
To find the value of "x", we must use this identity:

`cos\alpha=(adjacent)/(hypotenuse)`

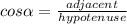
In this case:

`\alpha=30\°\\adjacent=x\\hypotenuse=RU=RS=4`

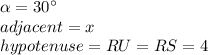
Substituting values and solving for "x", we get:

`cos(30\°)=(x)/(4)\\\\4*cos(30\°)=x\\\\x=√(12)`