Question

Please help with #12

Answer 1

a. 1 1/8 b. 8/9

Explanation:

You can set this up as a proportion to solve. For part a. we know that 2/3 of the road is 3/4 mile long. 2/3 + 1/3 = the whole road, so we need how many miles of the road is 1/3 its length. Set up the proportion like this:

`((2)/(3) )/((3)/(4) ) =((1)/(3) )/(x)`

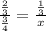
Cross multiplying gives you:

`(2)/(3)x=(1)/(3)*(3)/(4)`

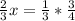
The 3's on the right cancel out nicely, leaving you with

`(2)/(3)x=(1)/(4)`

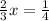
To solve for x, multiply both sides by 3/2:

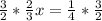`(3)/(2)*(2)/(3)x=(1)/(4)*(3)/(2)` gives you

`x=(3)/(8)`

That means that the road is still missing 3/8 of a mile til it's finished. The length of the road is found by adding the 3/4 to the 3/8:

`(3)/(4)+(3)/(8)=(6)/(8)+(3)/(8)=(9)/(8)`

So the road is a total of 1 1/8 miles long.

For b. we need to find out how much of 1 1/8 is 1 mile:

1 mile = x * 9/8 and

x = 8/9. When 1 mile of the road is completed, that is 8/9 of the total length of the road completed.