Question

Because of Theorem 5.47 any function that is continuous on (0, 1) but unbounded cannot be uniformly continuous there. Give an example of a continuous function on (0, 1) that is bounded, but not uniformly continuous.

Answer 1

`f: (0,1) \to \mathbb{R}`

`f(x) = \sin(1/x)`

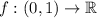
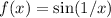
Explanation:

f is continuous because is the composition of two continuous functions:

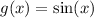`g(x) = \sin(x)` (it is continuous in the real numbers)

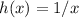`h(x) = 1/x` (it is continuous in the domain (0,1))

It is bounded because
`-1 \leq \sin(\theta) \leq 1`

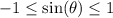
And it is not uniformly continuous because we can take
`\varepsilon = 1` in the definition. Let
`\delta > 0` we will prove that there exist a pair
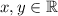`x,y\in \mathbb{R}` such that
`|x-y|< \delta` and
`|f(x) -f(y)|> \varepsilon = 1`.

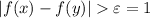Now, by the archimedean property we know that there exists a natural number N such that

`(1)/(N) < 2\pi \delta`

`\Rightarrow (1)/(2\pi N) < \delta`.

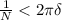
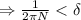Let's take
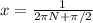`x = (1)/(2\pi N + \pi/2)` and
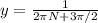`y = (1)/(2\pi N + 3\pi/2)`. We can see that

`|x-y| = (1)/(2\pi N + \pi/2)-(1)/(2\pi N + 3\pi/2)<(1)/(2\pi N) <\delta`

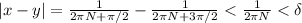
And also:

`|f(x)- f(y)| = |f(2\pi N + \pi/2) - f(2\pi N + 3\pi/2)| = |1 - (-1)| = 2 > \varepsilon`

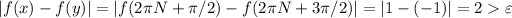
And we conclude the proof.