Answer:
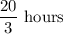
Explanation:
Let x be the speed of slower pump and 1.5x be the speed of faster pump to fill the swimming pool .
Then , According to the given question, we have the following equation:-
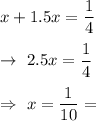
Now, the time taken by faster pump to fill the pool is given by :-
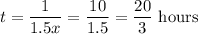
Hence, the faster pump would take
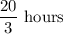 to fill the pool if it had worked alone at its constant rate.
to fill the pool if it had worked alone at its constant rate.