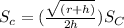Question

he volume of a cone of radius r and height h is​ one-third the volume of a cylinder with the same radius and height. Does the surface area of a cone of radius r and height h equal​ one-third the surface area of a cylinder with the same radius and​ height? If​ not, find the correct relationship. Exclude the bases of the cone and cylinder.

Answer 1

The surface area of a cone of radius r and height h not equal​ to one-third the surface area of a cylinder with the same radius and​ height.

Relationship is
`S_c=((√((r+h)))/(2h))S_C`

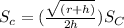
Explanation:

Given : The volume of a cone of radius r and height h is​ one-third the volume of a cylinder with the same radius and height.

To find : Does the surface area of a cone of radius r and height h equal​ one-third the surface area of a cylinder with the same radius and​ height?

If​ not, find the correct relationship. Exclude the bases of the cone and cylinder.

Solution :

Radius of cone and cylinder is 'r'.

Height of cone and cylinder is 'h'.

The volume of cone is
`V_c=(1)/(3)\pi r^2 h`

The volume of cylinder is
`V_C=\pi r^2 h`

`(V_c)/(V_C)=((1)/(3)\pi r^2 h)/(\pi r^2 h)`

`V_c=(1)/(3)V_C`

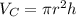
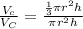
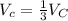
i.e. volume of cone is one-third of the volume of cylinder.

Now,

Surface area of the cone is
`S_c=\pi r√((r+h))`

Surface area of the cylinder is
`S_C=2\pi rh`

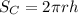
Dividing both the equations,

`(S_c)/(S_C)=(\pi r√((r+h)))/(2\pi rh)`

`(S_c)/(S_C)=(√((r+h)))/(2h)`

`S_c=((√((r+h)))/(2h))S_C`

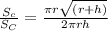
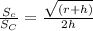
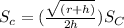
Which clearly means
`S_c\\eq (1)/(3)S_C`

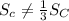
i.e. The surface area of a cone of radius r and height h not equal​ to one-third the surface area of a cylinder with the same radius and​ height.

The relationship between them is

`S_c=((√((r+h)))/(2h))S_C`