Question

A spotlight on the ground shines on a wall 12 m away. If a man 2 m tall walks from the spotlight toward the building at a speed of 1.7 m/s, how fast is the length of his shadow on the building decreasing when he is 4 m from the building?

Answer 1

0.6375 m/s

Step-by-step explanation:

Let x be the distance of the man from the building

from the figure attached

initially the value of x=12

Given:

`(dx)/(dt)=-1.7m/s`

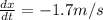
where the negative sign depicts that the distance of the man from the building is decreasing.

Now, Let The length of the shadow be = y

we have to calculate
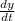`(dy)/(dt)` when x=4

from the similar triangles

we have,

`(2)/(12-x)=(y)/(12)`

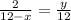
or

`y=(24)/(12-x)`

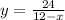
Differentiating with respect to time 't' we get

`(dy)/(dt)=-(24)/(12-x)^2(-dx)/(dt)`

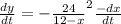
or

`(dy)/(dt)=(24)/(12-x)^2(dx)/(dt)`

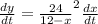
Now for x = 4, and
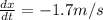`(dx)/(dt)=-1.7m/s` we have,

`(dy)/(dt)=(24)/(12-4)^2* (-1.7)`

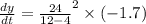
or

`(dy)/(dt)=-0.6375m/s`

here, the negative sign depicts the decrease in length and in the question it is asked the decreasing rate thus, the answer is 0.6375m/s