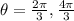Answer:

Explanation:
You need 2 things in order to solve this equation: a trig identity sheet and a unit circle.
You will find when you look on your trig identity sheet that

so we will make that replacement, getting everything in terms of sin:
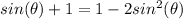
Now we will get everything on one side of the equals sign, set it equal to 0, and solve it:
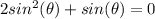
We can factor out the sin(theta), since it's common in both terms:

Because of the Zero Product Property, either
 or
or
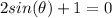
Look at the unit circle and find which values of theta have a sin ratio of 0 in the interval from 0 to 2pi. They are:
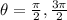
The next equation needs to first be solved for sin(theta):
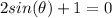 so
so
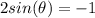 and
and

Go back to your unit circle and find the values of theta where the sin is -1/2 in the interval. They are: