Answer with Step-by-step explanation:
We are given that u and v are a basis for the two dimensional vector space.
To prove that w=u+v and x=u-v is also a basis .
By using matrix we prove w and x are basis of vector space.
We make a matrix from w and x
![\left[\begin{array}{cc}1&1\\1&-1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/2gqxdykam8l0wt9br8ua359fzy5psjhg2m.png)
Apply operation
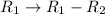
![\left[\begin{array}{cc}0&2\\1&-1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/d7t8hvjg53f4p7hihvo4ph9hw5gdnexxlo.png)
Apply
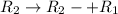
![\left[\begin{array}{cc}0&2\\1&1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/9i4ygfmuiai9qmhx5j0wknn3y3b5fcegun.png)
Apply
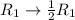
![\left[\begin{array}{cc}0&1\\1&1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/3segd0afmjnsijhi9nfgduk33qbinfqsnd.png)
Apply

![\left[\begin{array}{cc}0&1\\1&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/uqz5icz0wly9rkc0o862643r68hetder13.png)
Rank is 2 .Therefore, row one and second row are linearly independent.
Hence, first and second row are linearly independent because, any row is not a linear combination of other row.
Therefore, w and x are formed basis of given vector space.