Question

There are two newborns, Gary and Eric. The future lifetime of Gary is uniformly distributed between 0 to 60 years. The future lifetime of Eric is uniformly distributed between 0 to 40 years. Their future lifetimes are independent. Calculate the probability that Gary dies first.

Answer 1

Answer: 0.25

Explanation:

Given : The future lifetime of Gary is uniformly distributed with interval [0 years , 60 years].

Then the probability density function for Gary's future lifetime will be:-

`f(x)=(1)/(60-0)=(1)/(60)`

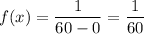
The future lifetime of Eric is uniformly distributed with interval [0 years , 40 years].

Then the probability density function for Erin's future lifetime will be:-

`f(x)=(1)/(40-0)=(1)/(40)`

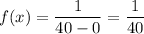
Now, the joint density function for Gary and Eric's future lifetime :-

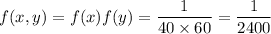`f(x,y)=f(x)f(y)=(1)/(40*60)=(1)/(2400)` [∵Their future lifetimes are independent. ]

Now, the probability that Gary dies first is given by :-

`\int^(60)_(0)\int^(40)_(x)f(x,y)\ dy\ dx\\\\=\int^(60)_(0)\int^(40)_(x)(1)/(2400)\ dy\ dx\\\\=\int^(60)_(0)(40-x)/(2400)\ dx\\\\=(1)/(2400)[40x-(x^2)/(2)]^(60)_(0)\\\\=(1)/(2400)(2400-(3600)/(2))=0.25`

Hence, the probability that Gary dies first =0.25