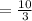Question

Soda Q is bottled at a rate of 500 liters/second, 24 hours a day. Soda V is bottled at a rate of 300 liters/second, 24 hours a day. If twice as many bottles of Soda V as of Soda Q are filled in a day, what is the ratio of the volume of a bottle of Soda Q to a bottle of Soda V?

Answer 1

`(10)/(3)`

Explanation:

Let x be the filled bottles of soda Q,

As per statement,

The filled bottles of soda V = 2x,

Given,

Rate of filling of soda Q = 500 liters per sec,

So, the total volume filled by soda Q in a day = 500 × 86400 = 43200000 liters,

( ∵ 1 day = 86400 second ),

Thus, the volume of a bottle of Soda Q =
`\frac{\text{Total volume filled by soda Q}}{\text{filled bottles of soda Q}}`

`=(43200000)/(x)`

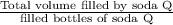
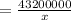
Now, rate of filling of soda V = 300 liters per sec,

So, the total volume filled by soda V in a day = 300 × 86400 = 25920000 liters,

Thus, the volume of a bottle of Soda V

`=(25920000)/(2x)`

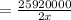
Thus, the ratio of the volume of a bottle of Soda Q to a bottle of Soda V

`=((43200000)/(x))/((25920000)/(2x))`

`=(10)/(3)`