Question

Two wires are perpendicular to each other and form a coordinate axis. The current in the vertical wire is going up (in the positive y direction) and the current in the horizontal wire is going to the right(in the positive x direction). Where is the net magnetic field equal to zero?

Answer 1

Magnetic field shall be zero at exactly in between the wires.

Step-by-step explanation:

We can find the magnetic field by biot Savart law as follows

`\overrightarrow{dB}=(\mu _(0)I)/(4\pi )\int \frac{\overrightarrow{dl}* \widehat{r}}{r^(2)}`

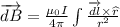
For current carrying wire in positive y direction we have

`\overrightarrow{dB_(1)}=(\mu _(0)Idl)/(4\pi )\int \frac{\widehat{j}* \widehat{r_(1)}}{r_(1)^(2)}`

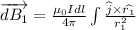
Similarly for wire carrying current in -y direction we have
`\overrightarrow{dB_(2)}=(-\mu _(0)Idl)/(4\pi )\int \frac{\widehat{j}* \widehat{r_(2)}}{r_(2)^(2)}`

Thus the net magnetic field at any point in space is given by

`\overrightarrow{dB_(1)}+\overrightarrow{dB_(2)}`

`(\mu _(0)Idl)/(4\pi )\int \frac{\widehat{j}* \widehat{r_(1)}}{r_(1)^(2)}+(-\mu _(0)Idl)/(4\pi )\int \frac{\widehat{j}* \widehat{r_(2)}}{r_(2)^(2)}=0\\\\\Rightarrow \overrightarrow{r_(1)}=\overrightarrow{r_(2)}`

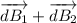
For points with same position vectors from the 2 wires we have a net zero magnetic field. These points are exactly midway between the 2 wires