Question

The production department of Celltronics International wants to explore the relationship between the number of employees who assemble a subassembly and the number produced. As an experiment, 2 employees were assigned to assemble the subassemblies. They produced 11 during a one-hour period. Then 4 employees assembled them. They produced 18 during a one-hour period. The complete set of paired observations follows.

Number of Assemblers One-Hour Production (units)
2 11
4 18
1 7
5 29
3 20
The dependent variable is production; that is, it is assumed that different levels of production result from a different number of employees.
a. Draw a scatter diagram.
b. Based on the scatter diagram, does there appear to be any relationship between the number of assemblers and production? Explain.
c. Compute the correlation coefficient.

Answer 1

We are given that The dependent variable is production; that is, it is assumed that different levels of production result from a different number of employees.

Number of Assemblers(x) One-Hour Production(y) (units)

2 11

4 18

1 7

5 29

3 20

a. Draw a scatter diagram.

Solution : Refer the attached figure

b. Based on the scatter diagram, does there appear to be any relationship between the number of assemblers and production? Explain.

Solution: The equation that shows the relationship between the number of assemblers and production is
`y=5.1x+1.7`

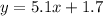
Where y is One-Hour Production (units) and x is the Number of Assemblers

c.Compute the correlation coefficient.

Solution:

Formula of correlation coefficient:
`r=(n(\sum xy)-(\sum x)(\sum y))/([n \sum x^2 -(\sum x)^2][n \sum y^2 -(\sum y)^2])`

x y xy
`x^2`
`y^2`

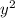
2 11 22 4 121

4 18 72 16 324

1 7 7 1 49

5 29 145 25 841

3 20 60 9 400

Sum: 15 85 306 55 1735

n=5

Substitute the values in the formula :

`r=(5(306)-(15)(85))/([5 (55) -(15)^2][5 (1735) -(85)^2])`

`r=0.00351`

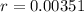
The correlation coefficient is 0.00351