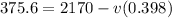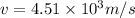Answer:
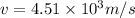
Step-by-step explanation:
electric field = 2170 N/C
now the speed of the charge particle is given as
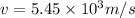
here we know that charge particle moves without any deviation
so we will have
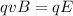
now magnetic field in this region is given as
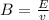
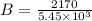
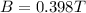
Now another charge particle enters the region with different speed and experience the force upwards
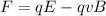
![1.54 * 10^(-9) = (4.10* 10^(-12))[2170 - v(0.398)]](https://img.qammunity.org/2020/formulas/physics/college/2r42f2a6ojm1g9ft2nyvt3uewf9a8plt30.png)