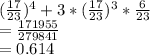Question

In a given week, it is estimated that the probability of at least one student becoming sick is 17/23. Students become sick independently from one week to the next. Find the probability that there are at least 3 weeks of no sick students before the 2nd week of at least one sick student.

Answer 1

0.614

Explanation:

Let the time be given by = t

and P(S ) = probability that a person is sick

P(s) = probability that a person is not sick

P(s) =
`((17)/(23))^(23)* (1-(17)/(23))\\`

Then the probability for that there are at least 3 weeks of no sick students before the 2nd week of at least one sick student is given by:

`((17)/(23))((17)/(23))((17)/(23))((17)/(23)) + (6)/(23) + 3((17)/(23))^(3)\\ = 0.614`

Answer 2

`0.614`

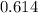
Explanation:

Let us suppose a time period "t" which is greater than 4 weeks.

Let us say

`X = 1` for no sick student

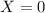`X = 0` for sick student

Now the probability of at no sick student each week is given by

P
`= {1,1, 1,1}`

`((17)/(23))^4`

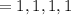
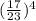
There are other cases such as

`(1,1,1,0),(1,1,0,1),(1,0,1,1),(0,1,1,1)`

The probability of above cases is equal to

`((17)/(23))^3*(1-(17)/(23))\\= ((17)/(23))^3 * (6)/(23)`

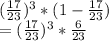
Now the probability of that there are at least 3 weeks of no sick students before the 2nd week of at least one sick student

=
`((17)/(23))^4 + 3*((17)/(23))^3* (6)/(23) \\= (171955)/(279841) \\= 0.614`