Question

If u(x)=-2x^2+3 and (x)=1/x, what is the range of (u°v)(x)​

Answer 1

The range is all real number y<3.

Explanation:

`(u \circ v)(x)=u(v(x))`

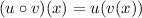
So we have to have v(x) exist for input x.

Let's think about that. v(x)=1/x so the domain is all real numbers except 0 since you cannot divide by 0. v(x)=1/x will also never output 0 because the numerator of 1/x is never 0. So the range of v(x)=1/x is also all real numbers except y=0.

Now let's plug v into u:

`u(x)=-2x^2+3`

`u(v(x))=u((1)/(x)`

`u(v(x))=-2((1)/(x))^2+3`

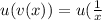
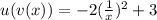
The domain of will still have the restrictions of v; let's see if we see any others here.

Nope, there are no, others, the only thing that is bothering this function is still the division by x (which means we can't plug in 0).

`u(v(x))=(-2)/(x^2)+3`

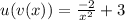
Let's thing about what are y's value will not ever get to be.

Let's start with that fraction. -2/x^2 will never be 0 because -2 will never be 0.

So we will never have y=0+3 which means y will never be 3.

There is one more thing to notice -2/x^2 will never be positive because x^2 is always positive and as we know a negative divided by a positive is negative.

So we have (a always negative number) + 3 this means the range will only go as high as 3 without including 3.

The range is all real number y<3.