Question

HELP!!!!! 35 POINTS ASAP!!!!!!!!!!!

Tension wires are attached from the top of a festival sign to the ground,
3
meters from the base of the sign. The angle of depression from the top of the sign to the point where one of the tension wires is attached to the ground is
28°
. How tall is the sign? Round to the nearest tenth.
The sign is __________ meters tall

Answer 1

1.6 m

Explanation:

The side of the sign, the ground, and the wire form a right triangle where the wire is the hypotenuse.

The angle of depression plus the upper interior angle of the triangle add to 90 degrees. That means that the upper acute angle of the triangle measures 90 - 28 = 62 deg.

Call the upper acute angle of the triangle Angle A and the height of the sign h.

tan A = opp/adj

tan 62 = 3/h

h tan 62 = 3

h = 3/tan 62

h = 1.6

Answer: 1.6 m

Answer 2

The tall of the sign board is 1.6 m.

Explanation:

Let's draw a diagram to represents the given situation.

In the diagram, the base of the festival sign to the ground forms 90°. So it is right triangle.

The angle of depression is 28°. The angle of the upper interior angle = 90° - 28° = 62°.

Now we can use the trigonometric ration "tan =
`(Oppsoite)/(Adjacent)`" and the height of the sign board.

Let's take "h" be the height/tall of the sign board.

As you can see in the diagram, the opposite side = 3m

Now plug in the given values in the tan ratio, we get

tan 62° =
`(3)/(h)`

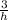
The value of tan 62° = 1.88

So, 1.88 =
`(3)/(h)`

h =
`(3)/(1.88)`

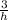
h = 1.595

We are asked to round of the nearest tenths place.

So, h = 1.6 m

Therefore, the tall of the sign board is 1.6 m.