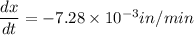Answer:
Decreasing rate of thickness when x=3 in is
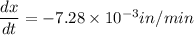
Step-by-step explanation:
Lets assume that thickness of ice over the spherical iron ball =x
So radius diameter of Sphere=5+x in
Inner radius=5 in
So volume V=
![(4)/(3)\pi [(5+x )^3-5^3]](https://img.qammunity.org/2020/formulas/physics/high-school/ktzvvrifn8xlgfsz2emnzjfsergcbm1za1.png)
V=
![(4)/(3)\pi [x^3+75x^2+15x]](https://img.qammunity.org/2020/formulas/physics/high-school/u1fcn1rfncwo796rscs8hirvudfp27xdpl.png)
Now given that ice melts rate=
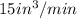
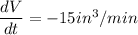
/(dt)](https://img.qammunity.org/2020/formulas/physics/high-school/6zms42n5wost8cs5fxefyldxkire2vj5ps.png)
When x=3 in
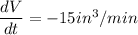
/(dt)](https://img.qammunity.org/2020/formulas/physics/high-school/oed2vjiqv4nvpnim3ct8zhpt4ht8nfciw5.png)
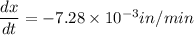
So decreasing rate of thickness when x=3 in is