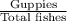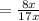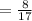Question

A large aquarium contains only two kinds of fish, guppies and swordtails. If 3/4​​ of the number of guppies is equal to 2/3​​ of the number of swordtails, then what fraction of fish in this aquarium are guppies?

Answer 1

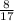`(8)/(17)` of fish in this aquarium are guppies.

Explanation:

Let x be the number of guppies and y be the number of swordtails in the aquarium,

According to the question,

`(3)/(4)\text{ of } x=(2)/(3)\text{ of }y`

`(3x)/(4)=(2y)/(3)`

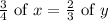
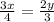
By cross multiplication,

`9x=8y`

`\implies (x)/(y)=(8)/(9)`

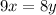
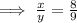
Thus, the ratio of guppies and swordtail fishes is 8 : 9

Let guppies = 8x, swordtail = 9x

Where, x is any number,

Since, the aquarium contains only two kinds of fish, guppies and swordtails,

So, the total fishes = 8x + 9x = 17x

Hence, the fraction of fish in the aquarium are guppies =
`\frac{\text{Guppies}}{\text{Total fishes}}`

`=(8x)/(17x)`

`=(8)/(17)`