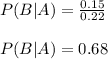Question

A basketball player can make make basket 70% of the time in the first Free Throw. However, if she misses the first one the conditional probability that she will make the second one is only 50%. If she makes the first one, then the chances of making the 2nd one is actually 90%. She made two attempts. a) Find the probability that she will make it both the times. b) Find the probability that she will make it exactly once. c) Given than she made it exactly once, what is the probability that it was the 2nd one?

Answer 1

Part a) 0.63

Part b) 0.22

Part c) 0.68

Explanation:

The individual probabilities are calculated as

1) Probability of scoring in first attempt = 70%

2) Probability of missing in first attempt = 30%

3) Probability of scoring in second attempt provided she scores in first attempt = 90%

4) Probability of missing in second attempt provided she scores in first attempt = 10%

5) Probability of scoring in 2nd attempt provided she misses in ist attempt = 50%

6) Probability of missing in 2nd attempt provided she misses in ist attempt = 50%

Part a)

probability of making the throw exactly both the times =
`P(ist)* P (2nd)`

Applying values we get

probability of making the throw exactly both the times=
`0.7* 0.9=0.63`

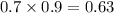
Part b)

She will make it exactly once if

1) She scores in first attempt and misses second

2) She misses in first attempt and scores in the second attempt

Probability of case 1 =
`0.7* 0.1=0.07`

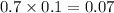
Probability of case 2 =
`0.3 * 0.5 =0.15`

Thus probability She will make it exactly once equals
`0.15+0.07=0.22`

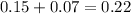
Part c)

It is a case of conditional probability

Now by Bayes theorem we have

`P(B|A)=(P(B\cap A))/(P(A))`

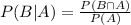
P(B|A) is the probability of scoring in second attempt provided that she has scored only once

P(B) is the probability of scoring exactly once

Given that she makes it exactly once
`\therefore P(A)=0.22`

`P(B\cap A)=0.15`

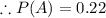
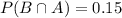
using these values we have

`P(B|A)=(0.15)/(0.22)\\\\P(B|A)=0.68`