Question

Z varies directly with x and inversely with y. What happens to Z when both x and y are doubled? z stays the same. z is halved. z doubles. z is squared.

Answer 1

z stays the same

Explanation:

We have been given that z varies directly with x and inversely with y.

Thus, we have the equation

`z=(kx)/(y)...(i)`

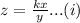
Here k is constant of proportionality.

Now, x and y both are doubled, thus, the equation becomes

`z=(k(2x))/(2y)`

Cancel 2 from numerator and denominator

`z=(kx)/(y)`

This is same as equation (i)

Hence, we can conclude that z remains same.

first option is correct.

Answer 2

z stays the same

Explanation:

From the statements

z ∝ x and z ∝ 1/y

Combining both proportions

z ∝ x/y

z = k * (x/y)

The above equation defines the relationship between x,y and z

k is the proportionality constant.

Lets say that x and y are doubled

Then

z = k * (2x/2y)

2 in the numerator and denominator will be cancelled out

z = k * (x/y)

Therefore we can conclude that z will stay the same if x and y are doubled ..