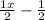Question

What is the inverse of the function f(x)= 2x+1​

Answer 1

In order to invert a function, switch y and x in the definition, and solve for y again:

`y=2x+1 \mapsto x=2y+1`

Solving for y, we have

`x=2y+1\iff x-1=2y \iff y=(x-1)/(2)`

Answer 2

h(x) =
`(1x)/(2) -(1)/(2)`

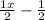
Explanation:

Given : f(x)= 2x+1​

To find : what is the inverse of the function .

Solution : We have given

f(x)= 2x+1​

To find the inverse of the function :

Step 1: take y = f(x)

y = 2x + 1

Step 2: interchange the x and y

x = 2y +1.

Step 3: Solve for y

On subtracting both sides by 1

x -1 = 2y.

On dividing both sides by 2

y =
`(x-1)/(2)`.

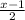We can write

y=
`(1x)/(2) -(1)/(2)`

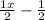
Step 4 : take y = inverse of f(x) = h(x)

h(x) =
`(1x)/(2) -(1)/(2)`

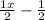
Therefore, h(x) =
`(1x)/(2) -(1)/(2)`