Question

A boat race runs along a triangular course marked by buoys A, B, and C. The race starts with the boats headed west for 3700 meters. The other two sides of the course lie to the north of the first side, and their lengths are 1700 meters and 2900 meters. Draw a figure that gives a visual representation of the situation. Then find the bearings for the last two legs of the race.

Answer 1

The last two bearings are

49.50° and 104.02°

Step-by-step explanation:

Applying the Law of cosine (refer to the figure attached):

we have

x² = y² + z² - 2yz × cosX

here,

x, y and z represents the lengths of sides opposite to the angels X,Y and Z.

Thus we have,

`cos X=(x^2-y^2-z^2)/(-2yz)`

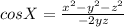
or

`cos X=(y^2 + z^2-x^2)/(2yz)`

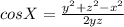
substituting the values in the equation we get,

`cos X=(2900^2 + 3700^2-1700^2)/(2* 2900* 3700)`

or

`cos X=0.8951`

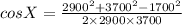
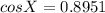
or

X = 26.47°

similarly,

`cos Y=(1700^2 + 3700^2-2900^2)/(2* 1700* 3700)`

or

`cos Y=0.649`

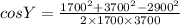
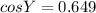
or

Y = 49.50°

Consequently, the angel Z = 180° - 49.50 - 26.47 = 104.02°

The bearing of 2 last legs of race are angels Y and Z.