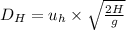Question

A rescue plane flying horizontally at spots a survivor in the ocean directly below and releases an emergency kit with a parachute. Because of the shape of the parachute, it experiences insignificant horizontal air resistance. If the kit descends with a constant vertical acceleration of how far away from the survivor will it hit the waves?

Answer 1

It covers a distance of
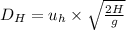`D_(H)=u_(h)* \sqrt{(2H)/(g)}` where symbols have the usual meanings.

Step-by-step explanation:

As shown in the figure

Let the height of aircraft be H meters above ground

Let it's horizontal flying velocity be
`v_(f)`

Using second equation of motion we can find the time it takes for the packet to reach the ground.

We have

`H=ut+(1)/(2)gt^(2)\\\\t=\sqrt{(2H)/(g)}\because (u=0)`

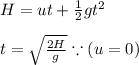
Thus horizantal distance covered in this time =
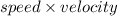`speed* velocity` Since there is no horizantal accleration

Thus horizantal distance it covers =
`D_(H)=u_(h)* \sqrt{(2H)/(g)}`