Answer:
0.077 to 0.24
Explanation:
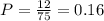
confidence level =95%=0.95
significance level =1-confidence level =1 -0.95= 0.05
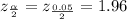 from the z table
from the z table
standard error of P
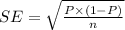
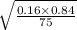 as n=75 given
as n=75 given
=0.0423
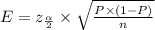
=1.96×0.0423=0.0289
now confidence interval is given by (0.16-0.0289 ,0.16+0.0289)
=(0.077,0.24)