Answer:
a)
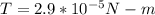
b) north edge will rise up
Step-by-step explanation:
torque on the coil is given as
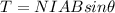
where N is number of loop = 9 loops
i is current = 7.80 A
-B -earth magnetic field =

A- area of circular coil

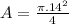
A =0.015 m2
PUTITNG ALL VALUE TO GET TORQUE

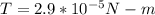
b) north edge will rise up