Answer:
Volume of the frustum is 76 unit³
Explanation:
From the figure attached we have to calculate the volume of the frustum formed by cutting off a square pyramid from the top.
Volume of the frustum =

Since ΔAPO' and ΔAOQ are similar so

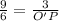
O'P =
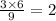 units
units
Therefore, side MN = 2× O'P = 4 units
Now we put these values in the formula
Volume of the frustum =

=
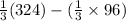
=
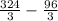
=
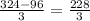
= 76 unit³