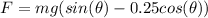Question

A child is sliding a toy block (with mass = m) down a ramp. The coefficient of static friction between the block and the ramp is 0.25. When the block is halfway down the ramp, the child pushes down on the block perpendicular to the plane, halting it. What is the minimum force the child must apply to keep the block from starting to slide down the ramp?

Answer 1

`F = (mgsin\theta)/(\mu) - mgcos\theta`

Step-by-step explanation:

As we know that the force applied is perpendicular to inclined plane

So here the normal force on the block is given as

`N = F + mgcos\theta`

now in order to stop the block by the perpendicular force we can say that the friction force is sufficiently large to balance the force of gravity

So here we can say

`F_f = mgsin\theta`

`\mu N = mgsin\theta`

`\mu(F + mg cos\theta) = mg sin\theta`

now we have

`F = (mgsin\theta)/(\mu) - mgcos\theta`

Answer 2

`F=mg(sin(\theta )-0.25 cos(\theta ))`

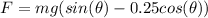
Step-by-step explanation:

The free body diagram of the block on the slide is shown in the below figure

Since the block is in equilibrium we apply equations of statics to compute the necessary unknown forces

N is the reaction force between the block and the slide

For equilibrium along x-axis we have

`\sum F_(x)=0\\\\mgsin(\theta )-\mu N-F=0\\\therefore F=mgsin(\theta)-\mu N......(\alpha )\\Similarly\\\sum F_(y)=0\\\\N-mgcos(\theta )=0\\\therefore N=mgcos(\theta ).......(\beta )\\\\`

Using value of N from equation β in α we get value of force as

`F=mg(sin(\theta )-\mu cos(\theta ))`

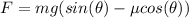
Applying values we get

`F=mg(sin(\theta )-0.25 cos(\theta ))`