Answer:
L = 3.391m
Step-by-step explanation:
a) Given:
Mass of the block, m = 205g=0.205kg
spring constant, k = 1.18 kN/m
Angle made by the ramp = 60°
displacement of the spring, x = 10cm= 0.1m
Now,
The initial potential energy of the spring = final gravitational potential energy of block
mathematically,
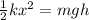
where,
g = acceleration due to gravity
h = height of the block above the ground = LsinΘ
L is the displacement of the block parallel to the ramp
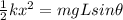
substituting the values in the above equation we get
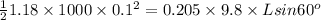
or
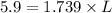
or
L = 3.391m