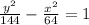Question

Which is the equation of a hyperbola centered at the origin with y-intercepts +12 -12, and asymptote y=3x/2

Pleaseeeee help meee

Answer 1

Answer: Answer D

\frac{y^2}{144}-\frac{x^2}{64}=1

Answer 2

`(y^2)/(144)-(x^2)/(64)=1`

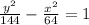
Explanation:

The equation of a hyperbola centered at the origin with vertices on the y-axis is given by:
`(y^2)/(a^2)-(x^2)/(b^2)=1`

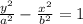
The vertices of the hyperbola are the y-intercepts (0,12) and (0,-12)

This implies that:

`2a=|12--12|`

`2a=24`

`a=12`

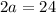
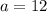
The asymptote equation of a hyperbola is given by:

`y=\pm(a)/(b)x`

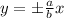
The given hyperbola has asymptote:
`y=\pm(3)/(2) x`

By comparison;
`(a)/(b)=(3)/(2)`

`\implies (12)/(b)=(12)/(8)`

`\implies b=8`

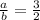
The required equation is:

`(y^2)/(12^2)-(x^2)/(8^2)=1`

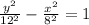
Or

`(y^2)/(144)-(x^2)/(64)=1`