Answer:
We choose D.
Explanation:
Let the midpoint is O
We will use Angle-SIde-Angle principle to prove that the diagonals of a rectangle bisect each other.
Have a look at the two triangles: AOB and DOC, they are congruent because:
- AB = DC
- ∠OAB = ∠DCO because they are alternate angles
- ∠OBA = ∠CDO because they are alternate angles
So we can conclude that: OB = OB when two triangles: AOB and DOC are congruent.
Similar, apply for the two triangles: AOD and BOC are congruent so we have OA = OC .
=> It proves that the point O simultaneously is the midpoint and intersection point for the diagonals.
=> The midpoint of AC is (
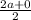 ,
,
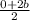 ) = (a, b), we choose D.
) = (a, b), we choose D.