Question

Prove that the diagonals of a rectangle bisect each other.

The midpoint of AC is _____

Answer 1

(a,b)

Explanation:

simply we find the midpoint of AC and the midpoint of Bd by dividing over 2

Answer 2

We choose D.

Explanation:

Let the midpoint is O

We will use Angle-SIde-Angle principle to prove that the diagonals of a rectangle bisect each other.

Have a look at the two triangles: AOB and DOC, they are congruent because:

• AB = DC
• ∠OAB = ∠DCO because they are alternate angles
• ∠OBA = ∠CDO because they are alternate angles

So we can conclude that: OB = OB when two triangles: AOB and DOC are congruent.

Similar, apply for the two triangles: AOD and BOC are congruent so we have OA = OC .

=> It proves that the point O simultaneously is the midpoint and intersection point for the diagonals.

=> The midpoint of AC is (
`(2a+ 0)/(2)` ,
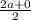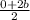`(0 + 2b)/(2)` ) = (a, b), we choose D.