Answer:
B. See explanation
Explanation:
Use the distance formula between two points
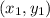 and
and
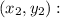
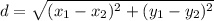
Find the lengths of all sides of quadrilateral DEFG:
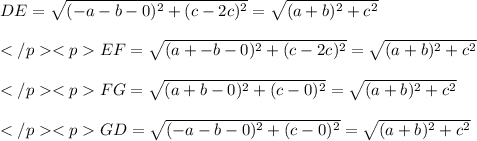
All sides are of the same length. Now fond the slopes of all sides:
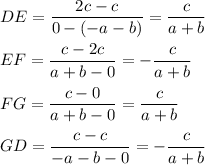
The slopes of the sides DE and FG are the same, so these sides are parallel. The slopes of the sides EF and GD are the same, so these sides are parallel.